Dans un sudoku, y a-t-il un minimum de cases préremplies ?

Oui. L’enjeu pour les journaux qui publient des sudokus est de proposer une grille qui, munie de cases préremplies et d’indices, ne pourra être complétée que d’une seule façon ; les lecteurs, à force de déduction, seront tous conduits à une solution unique.

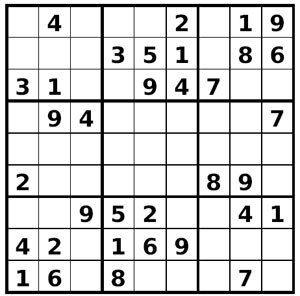
Rappelons que cette sorte de puzzle chiffré se compose d’une grille carrée de 9 cases de côté, soit 81 cases au total, subdivisée en 9 blocs de 3 cases de côté.Le principe est simple : remplir la grille de manière à ce que chaque rangée, chaque colonne et chacun des 9 blocs contiennent les chiffres de 1 à 9, en se servant des cases préremplies de chiffres.

Si en moyenne, un sudoku compte 25 indices, on sait que les grilles qui en contiennent seulement 16 peuvent toujours être complétées d’au moins deux façons, ce qui interdit leur publication ou n’en fait pas des défs acceptables. En revanche, dès 17 cases préremplies, on trouve des exemples de sudokus qui ne possèdent qu’une seule solution.

Le nombre minimal de cases préremplies est 17

Pour parvenir à ce chiffre de 17, le mathématicien Gordon Royle, de l’école d’informatique d’Australie occidentale, a épluché les quelque 50 000 grilles de sudoku de sa collection personnelle. Son constat : pas une seule ne comportait 16 cases préremplies. Les plus diaboliques ne descendant pas en dessous de 17 indices.

Afin de vérifer ce nombre, des mathématiciens de l’université de Dublin (Irlande) ont fait tourner un algorithme sur un superordinateur. Sa mission : remplir des grilles de 81 cases à 16 indices. Un travail de titan puisqu’il existe plus de 5,4 milliards de grilles possibles et pas moins de 34 millions de milliards de combinaisons d’indices à analyser pour chacune des grilles possibles.

Leur résultat, publié en 2012 dans la revue Nature, a montré qu’aucun des modèles de grille à 16 indices testés n’autorisait qu’une solution. CQFD !

Article source